2020-9-23

多角形の内外判定（javascriptでの実装を添えて）

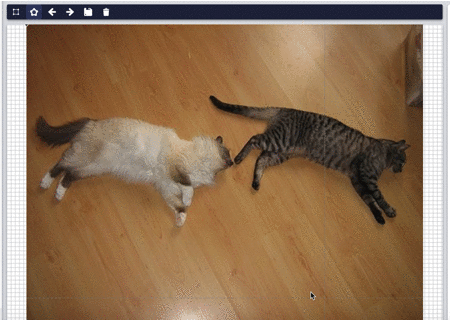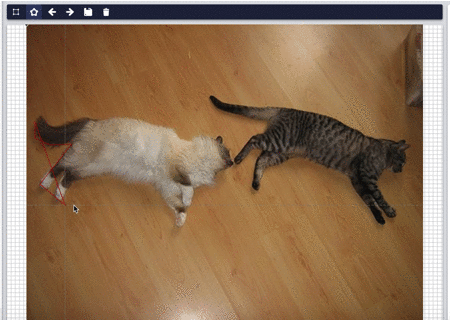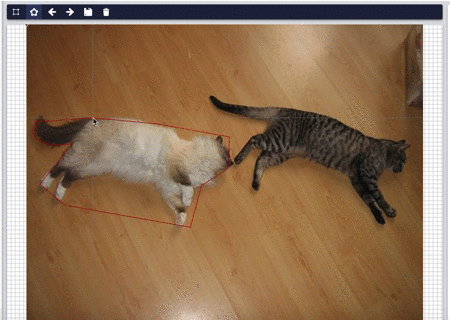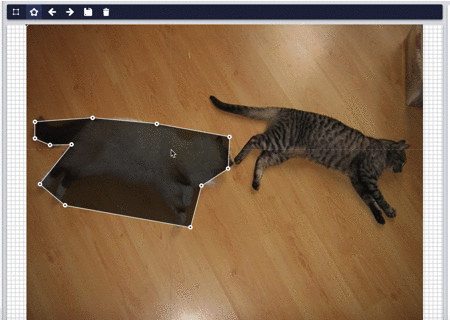
アノテーションツールでセグメンテーション用に多角形での範囲選択を実装しようとしている。四角形の場合には簡単に内外判定ができるが、多角形だとそう簡単にはいかない。今回実装にあたって多角形の内外判定を勉強した。

実装例

TL;DR

Winding Number Algorithmは割と楽に実装できる
実装するときは角度の符号の計算を忘れない

参考にした資料

理論だったり詳しい実装のポイントは以下の資料を見てください。この資料を見て理解できればこの記事は読まなくて大丈夫です。

www.nttpc.co.jp

Winding Number Algorighmとは

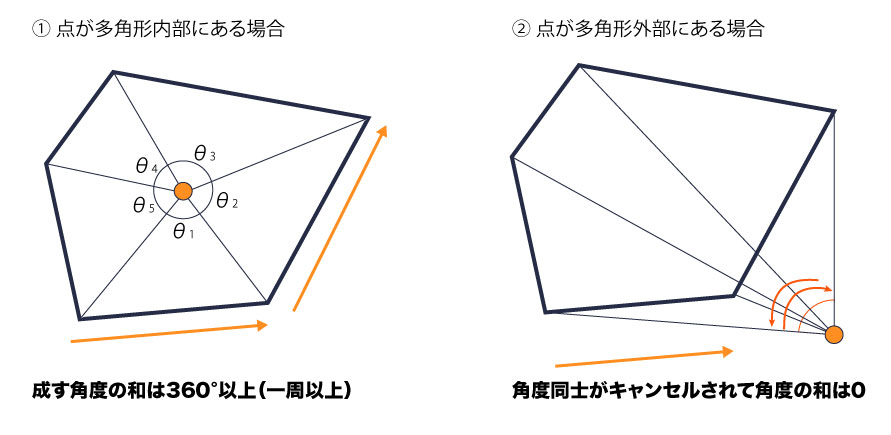
多角形の角２つと対象となる点が成す角度を順番に計算していき、それらの和が360°以上であれば（一周以上するのであれば）点は多角形内部にある。一方で和が0であれば、点は多角形外部にある。

最初角度の和が0になればってどういうこと？と悩んだが、角度を符号つきで計算すると外部にあるときは角度同士がキャンセルしあって和は0になるよ、と理解すれば良さそうだ。

「360°以上」というところは自己交差領域があると和が一周以上になる場合が出てくる（上記のNTTの資料参考）。あまり数学的なところは理解できないが他にありえるのだろうか。簡単な図解

実装する上での注意点

角度を符号付きで計算することを忘れなければ実装はかなり簡単。符号の計算を忘れるとうまく動かなくて沼にハマる。角度の絶対値はベクトルの内積を使えば簡単に計算できる。符号は外積を計算して、その符号だけを取ればOK。

javascriptでの実装

コメントを多めに入れたので長くなったが、やっていることは非常に簡単。バグがあれば教えてください。

 javascript 

                
              

                Copied!
              

              /\*\*
 \* 指定した点が多角形の中に含まれるかどうかを判定する
 \*
 \* @param {Array} polygon 多角形を構成する点（X, Y）の配列. 多角形を一周するように並んでいる必要がある.
 \* @param {Number} x 判定する点のX座標
 \* @param {Number} y 判定する点のY座標
 \* @returns {Boolean} 点が多角形に含まれていればtrue
 \*/
function hit(polygon, x, y) {
  let thetaSum = 0;
  const n = polygon.length;

  // i-1 => 指定された点 => i の成す角度の和をthetaSumに足し込んでいく
  for (let i = 1; i < n; i++) {
    if (polygon[i][0] === x && polygon[i][1] === y) {
      // 指定された点が多角形の角の場合うまく角度が計算できないので、判明した時点でtrueを返す
      return true;
    }
    const v1x = polygon[i - 1][0] - x;
    const v1y = polygon[i - 1][1] - y;
    const v2x = polygon[i][0] - x;
    const v2y = polygon[i][1] - y;
    thetaSum += computeDegree(v1x, v1y, v2x, v2y);
  }
  // 0とN番目の成す角度
  if (polygon[0][0] === x && polygon[0][1] === y) {
    return true;
  }
  const v1x = polygon[n - 1][0] - x;
  const v1y = polygon[n - 1][1] - y;
  const v2x = polygon[0][0] - x;
  const v2y = polygon[0][1] - y;
  thetaSum += computeDegree(v1x, v1y, v2x, v2y);
  thetaSum = Math.abs(thetaSum);

  if (thetaSum >= 0.1) {
    return true;
  }
  return false;
}

/\*\*
 \* ２つのベクトルの成す角度を符号付きで計算する
 \* 角度の絶対値の計算には内積を、符号の計算には外戚を利用する 
 \*
 \* @param {Number} x1 
 \* @param {Number} y1 
 \* @param {Number} x2 
 \* @param {Number} y2 
 \*/
function computeDegree(x1, y1, x2, y2) {
  const abs1 = Math.sqrt(x1*x1+y1*y1);
  const abs2 = Math.sqrt(x2*x2+y2*y2);
  let theta = Math.acos((x1*x2+y1*y2)/(abs1*abs2)); // 内積を使って角度を計算
  let sign = Math.sign(x1*y2-y1*x2); // 外積を使って符号を計算
  theta *= sign;
  return theta
}

function main() {
  const pol1 = [[0, 0], [100, 20], [100, 120], [0, 100]];
  // 通常の判定
  console.log(hit(pol1, 50, 50)); // true
  console.log(hit(pol1, 101, 50)); // false
  console.log(hit(pol1, 100, 121)); // false

  // コーナーケース（多角形の辺上の場合）
  console.log(hit(pol1, 50, 10)); // true
  console.log(hit(pol1, 100, 60)); // true

  // コーナーケース(多角形の角上の場合)
  console.log(hit(pol1, 0, 0)); // true
  console.log(hit(pol1, 100, 20)); // true
}

main();
            

nilci

blog

about