先日KaggleのAdTracking Competition に参加したが惨敗したため、特訓することにした。
Ad Tracking Competition で4位の人がFeature Engineeringについて非常にまとまった資料を公開していたので、その要約をまとめた。
勉強がてらPythonでサンプルコードを書いたので一緒においておく。
何故Feature Engineeringが必要なのか
価値のある特徴量を生成し、ノイズの原因となる特徴量を除去することでシンプルで精度のいいモデルを実現する。
たとえば下の図で、左の状態だと円形にプロットが分布していて、ニューラルネットワークやSVMなどの非線形モデルでないと分類することができない。
しかし各点を極座標で表して右のように変換すれば、非線形の手法を使わなくても決定木や線形分類器などのシンプルな手法で識別できるようになる。
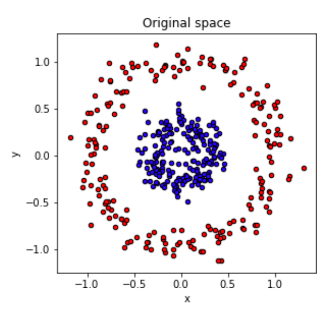
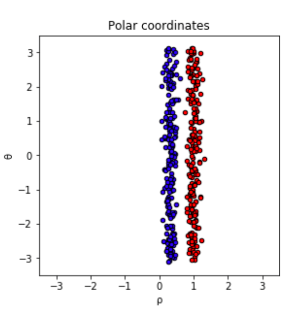
具体的な手法(カテゴリ変数の場合)
多くの機械学習手法(ニューラルネットワーク, svm)はカテゴリ変数を直接説明変数として利用することが難しい。
これらのモデルにカテゴリ変数を学習させたい場合には、カテゴリ変数を扱いやすい数値に変換する必要がある。
よりモデルがカテゴリ変数の意味を理解しやすいように様々な手法が考案されている。
カテゴリ変数の特徴(値に大小関係があるか、疎な入力でも問題がないか、特定の値だけが重要なのか)などを考えてどのような前処理を施すか決定することになる。
Label Encoding
単純にラベルを数字に置き換えるだけの処理。 多くの人が使ったことがあるのではないかと思う。下の例だとA→0、B→1、C→2という様に置き換えてる。pythonだとsklearnのLabelEncoderを使うのが楽。
| idx | category | encoded_feature |
| :---: | :---: | :---: |
| 0 | A | 0 |
| 1 | A | 0 |
| 2 | A | 0 |
| 3 | B | 1 |
| 4 | B | 1 |
| 5 | C | 2 |
import pandas as pd
from sklearn.preprocessing import LabelEncoder
df = pd.DataFrame({
"category" : ["A","A","A","B","B","C"],
})
le = LabelEncoder()
df["encoded\_feature"] = le.fit_transform(df["category"])
df.head(10)
One Hot Encoding
カテゴリ変数の各値ごとにカラムを分けて0、1で表現する方法。
下の例だとcategory_A, category_B, category_Cという列を新しく作って、Aの場合には(1, 0, 0)、Bの場合には(0, 1 ,0)、Cの場合には(0, 0, 1)と表現する。
ニューラルネットワークでカテゴリ変数を表すときはOne Hot Encodingが第一選択肢になる気がする。
LabelEncodingのときと同様、One Hot Encoderがsklearnに収録されているので、それを使うのが楽。
pandasにはget_dummiesというメソッドが収録されているので、それを使っても同じことが出来る。
| idx | category | category_A | category_B | category_C |
| :---: | :---: | :---: | :---: | :---: |
| 0 | A | 1 | 0 | 0 |
| 1 | A | 1 | 0 | 0 |
| 2 | A | 1 | 0 | 0 |
| 3 | B | 0 | 1 | 0 |
| 4 | B | 0 | 1 | 0 |
| 5 | C | 0 | 0 | 1 |
#one hot encoding sample
import pandas as pd
from sklearn.preprocessing import OneHotEncoder
df = pd.DataFrame({
"category" : ["A","A","A","B","B","C"],
})
#文字をLabel Encodingして数値に変換
le = LabelEncoder()
df["encoded\_feature"] = le.fit_transform(df["category"])
#One Hot Encoding
ohe = OneHotEncoder()
ohe_array = ohe.fit_transform(df[["encoded\_feature"]])
df.drop("encoded\_feature", axis = 1, inplace = True)
#DataFrameに変換
ohe_df = pd.DataFrame(ohe_array.todense()).astype("uint8")
ohe_df.columns = ["category\_A","category\_B","category\_C"]
#元のDataFrameと結合
df = pd.concat([df,ohe_df], axis = 1)
df.head(10)
Frequency Encoding
各値の出現頻度で表現する方法。例えば以下の表におけるAの値は、3(Aの出現回数)/ 6(全体の行数)で0.5となる。pandasを使えばgroupbyとmergeを駆使して比較的に簡単に書くことが出来る。
| idx | category | category_counts | frequency_encoding |
| :---: | :---: | :---: | :---: |
| 0 | A | 3 | 0.500000 |
| 1 | A | 3 | 0.500000 |
| 2 | A | 3 | 0.500000 |
| 3 | B | 2 | 0.333333 |
| 4 | B | 2 | 0.333333 |
| 5 | C | 1 | 0.166667 |
#Frequency Encoding Sample
import pandas as pd
from sklearn.preprocessing import OneHotEncoder
df = pd.DataFrame({
"category" : ["A","A","A","B","B","C"],
})
#各カテゴリーの出現回数を計算
grouped = df.groupby("category").size().reset_index(name='category\_counts')
#元のデータセットにカテゴリーをキーとして結合
df = df.merge(grouped, how = "left", on = "category")
df["frequency"] = df["category\_counts"]/df["category\_counts"].count()
df.head(10)
Target Mean Encoding
Likelihood Encodingとも呼ばれる。Google検索でのヒット数的にはTarget Mean Encodingの方がメジャー。あるカテゴリ変数の値を持ち目的変数が1の個数を、その値の出現回数で割ったもの。
下の例だと、Aの出現回数は3回、カテゴリーがAで目的変数が1を持つものの出現回数は2回なのでTarget Mean Encodingの値は2/3 = 0.666となる。
| idx | category | outcome | category_counts | outcome_counts | target_mean_encoding |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | A | 1 | 3 | 2 | 0.666667 |
| 1 | A | 1 | 3 | 2 | 0.666667 |
| 2 | A | 0 | 3 | 2 | 0.666667 |
| 3 | B | 1 | 2 | 1 | 0.500000 |
| 4 | B | 0 | 2 | 1 | 0.500000 |
| 5 | C | 1 | 1 | 1 | 1.000000 |
#Target Mean Sample
import pandas as pd
from sklearn.preprocessing import OneHotEncoder
df = pd.DataFrame({
"category" : ["A","A","A","B","B","C"],
"outcome" : [1,1,0,1,0,1],
})
単純に計算すれば次のようなコードになる。
#各カテゴリーともう一つの特徴量の出現回数を計算
grouped_category = df.groupby("category")["category"].count().reset_index(name='category\_counts')
grouped_outcome = df.groupby("category")["outcome"].sum().reset_index(name='outcome\_counts')
#元のデータセットにカテゴリーをキーとして結合
df = df.merge(grouped_category, how = "left", on = "category")
df = df.merge(grouped_outcome, how = "left", on = "category")
df["target\_mean\_encoding"] = df["outcome\_counts"]/df["category\_counts"]
df.head(10)
Target Mean Encodingには過学習を防ぐための leave one out schemaという手法も提案されている。
これは上の表で1列目のAに対してTarget Mean Encodingを計算するときに、自分自身の値を除いて計算する方法だ。
この方法を用いて1列目のAに対してTarget Mean Encoding を計算すると(自分を除いたカテゴリーがAで目的変数が1の総数) / (自分を除いたAの出現回数)= 0.5 となる。
| idx | category | outcome | category_counts | outcome_counts | target_mean_encoding |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | A | 1 | 3 | 2 | 0.5 |
| 1 | A | 1 | 3 | 2 | 0.5 |
| 2 | A | 0 | 3 | 2 | 1.0 |
| 3 | B | 1 | 2 | 1 | 0.0 |
| 4 | B | 0 | 2 | 1 | 1.0 |
| 5 | C | 1 | 2 | 2 | 1.0 |
| 6 | C | 1 | 2 | 2 | 1.0 |
#Target Mean Sample with leave one out scheme
import pandas as pd
from sklearn.preprocessing import OneHotEncoder
df = pd.DataFrame({
"category" : ["A","A","A","B","B","C","C"],
"outcome" : [1,1,0,1,0,1,1],
})
#各カテゴリーの出現回数を計算
grouped_category = df.groupby("category")["category"].count().reset_index(name='category\_counts')
grouped_outcome = df.groupby("category")["outcome"].sum().reset_index(name='outcome\_counts')
#元のデータセットにカテゴリーをキーとして結合
df = df.merge(grouped_category, how = "left", on = "category")
df = df.merge(grouped_outcome, how = "left", on = "category")
#計算する際に自分自身の値は除く
df["target\_mean\_encoding"] = (df["outcome\_counts"] - df["outcome"])/(df["category\_counts"] - 1)
df.head(10)
おわりに
4種類のカテゴリ変数の数値化に関する方法を紹介した。「カテゴリー変数に対する手法」という目次をつけておいて、時間が無くて数値変数に対する手法の紹介まで出来なかったのが申し訳ない。
もとのスライドには、Weight of Evidecneと呼ばれる手法や、具体的な特徴量抽出の手順などが記載されているので時間があったら追記するかもしれない。